1. はじめに

1.1. まえがき

この記事では、関数型プログラミングにおいて動的計画法(Dynamic Programming)を行う手法の一つである dynamorphism について解説します。

しかし、dynamorphism という概念はそれ単体で説明できるものではなく、F-代数 や catamorphism, anamorphism, hylomorphism, histmorphism などの各種概念を用いないと説明できないものです。そこでこの記事では順々とそれらの概念を追っていき、最後にdynamorphismに行き着くような構成になっています。

そのため、この記事は dynamorphism の説明記事であると同時に、F-(余)代数や catamorphism, anamorphism 等に関する解説記事でもあります。

ここで留意していただきたい点が何点かあります。いわゆる予防線です。

• 筆者はHaskellや圏論や型理論に関しては全くの素人¹です。そのため今回は付け焼き刃の曖昧な知識だけで記述した箇所が多くあります。そのため、各種概念の正確な定義などに関しては文献などをあたってもらえればと思います。また、間違いを見つけたらブログのコメント欄にでも指摘していただくと幸いです。

• この記事では圏論の知識はほとんど仮定しません。しかし圏論を少し知っておくと若干理解の助けになるとは思います。圏論に触れる際にオススメなのは、2013年に開かれたプログラマ向けの圏論勉強会の資料です。また、この記事全体では断りのない限りHask圏に限った話をしていきます。そのため「射」を「関数」、「対象」を「型」と表現しています。

• コードの例は Haskell を用いています。実行環境は OSX (El Capitan) の GHC 7.10.2 です。

• この文書は madoko を用いて生成されました。

また、先にこの記事を読んでいただければと思います。$1$ や $A+B$、$A \times B$ などがどのような意味を持つかを知っておくと理解が容易になると思います。

1.2. 記号や用語などの説明

$1$

Unit型。何も値がない(「空」という値のみを持つ)ことを表現するために用いられます。Haskell で言う ()

$A \times B$

型 $A$ と 型 $B$ の直積を意味します。つまり、型AとBの値両方を持つ型です。タプル と呼ばれることがあります。Haskell の場合は (A,B)。C/C++的に書くと struct { A a; B b; }。

$A + B$

型 $A$ と 型 $B$ の直和を意味します。つまり、型AとBの値どちらか一方を持つ型です。Haskell の場合は Either A B。C/C++的に書くと union { A a; B b; }²。

代数的データ型 (Algebraic Data Type)

直積と直和の組み合わせによって表現される型のことです。Haskell や OCaml などの他に、Rust や Swift などにも実装されています。

$f : A \to B$

Aを受け取ってBを返す関数を表します。

$\langle f, g\rangle$

任意の型 $X$ に対し、$f : X \to A, g : X \to B$ となるとき、$\langle f, g \rangle : X \to A \times B$ となる関数が一意に定義できます。これを f と g の積 (product of morphism) といいます。Haskellで実装すると、proj f g x = (f x, g x)となります。

$id_A$

型 A に関する恒等写像を表します。つまり、型 A の全ての値 x に対して $id_A(x) = x$ です。

2. 関手と不動点

木やリストなどのデータ構造は、再帰的定義 (recursive definition) によって表現されます。 再帰的定義とは、自分自身を定義に含めるものを言います。例えばリストの例で言うと、

• 空リスト (nil) はリストである。
• 値とリストのペア (cons) はリストである。

がリストの再帰的定義になります。 数学的(圏論的)にそのような再帰的データ構造を定式化すると、それは関手の不動点として定義されます。 ここで関手と不動点という概念が出てきました。それらについて見ていきましょう。

2.1. 関手

関手³とは、型 $A$ と関数 $f$ を、他の型 $F(A)$ と関数 $F(f)$ にマッピングするものです。このとき、関数のマッピングに関して以下の構造を保つ必要があります。

• 型 $X$ に関して、$ F(id_X) = id_{F(X)} $
• 関数 $f: X \to Y, g : Y \to Z$ に対して $ F(g \circ f) = F(g) \circ F(f) $

ざっくり言うと、関手とは型同士の関係を保つ写像であるといえます。Haskell ではそのまま Functor という型クラスで定義され、インスタンスとして List や Maybe などがあります。

さて、以下の関手を考えてみましょう。ここで、Intは整数型です。

これをHaskellのコードで表すと以下のようになります。

{- Nil が 1 を、Cons Int x が Int × X を表現している-}
data F x = Nil | Cons Int x

{- Fを関手のインスタンスにするための宣言、関数についてのマッピング -}
instance Functor F where
  fmap f Nil = Nil
  fmap f (Cons x xs) = Cons x (f xs)

以下の例を見れば分かる通り、$F(X)$ は一種のリストに対するコンストラクタ(構成子)となっています。 $Int \times X$ が Cons ペア、$1$が nil (リストの終端) を表現しています。

Nil :: F a
Cons 1 $ Nil :: F (F a)
Cons 1 $ Cons 2 $ Nil :: F (F (F a))
Cons 1 $ Cons 2 $ Cons 3 $ Nil :: (F (F (F (F a))))

しかし、このままではリストのサイズによって型が変わってしまいますし、型変数 a も残ったままです。 これを避けるために不動点の概念を導入します。

2.2. 不動点

そもそもリストを関手で表現したいならば、こう定義した方がよさそうに見えます。

しかしこれでは定義自身に${\sf List}$ が含まれる、いわゆる再帰的定義となってしまいます。

そこで、(2)を「方程式」とみなし、その方程式を満たすような ${\sf List}$ を「リストを表すデータ型」とする発想の転換をします。しかし、型同士の等式は $=$ ではなく 同型 $ \simeq $ で結びます。

つまり、次の「方程式」を満たすような $X$ が「リストを表すデータ型」です。

ここで、(1)より、(3)は次のように書けます。

この時、(4)を満たすような $X$ のことを関手$F$の不動点 とよび、$\mu F$ で表します。⁴そして $\mu F$ こそがまさに求めたい リストを表現するデータ型 となっています。

以下、Haskellへ不動点を導入した上で、先述のFに関して不動点を適用して、実際にリストを表現することを確認します。

{- 関手 f について不動点を取る
  ここで、 inF  :: f (FixF f) -> FixF f
                 outF :: FixF f     -> f (FixF f)
  であり、inF . outF = id, outF . inF = id
  よって同型の定義より f について不動点を取れている。-}
newtype FixF f = InF { outF :: f (FixF f) }

{- IntList = (F の不動点) -}
type IntList = FixF F

{- IntList を構成する補助関数 -}
nil :: IntList
nil = InF Nil
cons :: Int -> IntList -> IntList
cons a as = InF $ Cons a as

a0 = nil :: IntList
a1 = cons 1 $ nil :: IntList
a2 = cons 1 $ cons 2 $ nil :: IntList
a3 = cons 1 $ cons 2 $ cons 3 $ nil :: IntList

これで任意長の長さのリストを型 IntList = FixF F にまとめる事ができました。 つまり、関手 $F$ の不動点 $\mu F$ を取ることによって 任意の長さのリストを表現するデータ型 が作れました。

3. catamorphism と anamorphism

この章では catamorphism と anamorphism について説明します。 catamorphism は、関数型プログラミングでいう fold の一般化であり、データ構造を畳み込んで1つの値にする処理のことを表現しています。anamorphism はそれとは逆に、1つの値からデータ構造を構築する処理のことを表します。

catamorphism, anamorphism について定式化するため、代数と余代数という概念を導入します。これは圏論に由来するものであり、若干抽象的な話題になってきます。そこで、可換図式をいくつか載せました。可換図式によって何となくでも良いのでイメージを掴んでもらえればと思います。

3.1. 代数とcatamorphism

関手 $F$ について、型 $A$ と、関数 $f : F(A) \to A$ のペア $(A, f)$ を $F$-代数 (F-algebra) といいます。 また、F-代数 $(A, a : F(A) \to A), (B, b : F(B) \to B)$ に対し、$f : A \to B$ で $f \circ a = b \circ F(f)$ を満たすものをF-代数の準同型 (homomorphism of F-algebra) といいます。すなわち、以下の図式を可換にします。(可換図式において、始点と終点が同じと成るような道は、全て合成によって同じ結果になることを示します。)

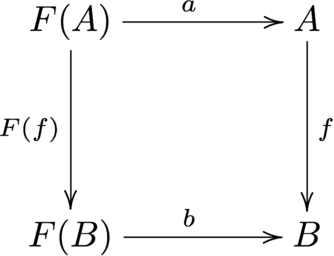
例として $ F(X) = 1 + {\rm Int} \times X $ のF-代数を挙げます。ここで $A = {\rm Int}$として F-代数 $(A,f)$ を考えると、関数 f の型は $F({\rm Int}) \to {\rm Int} $ つまり $ 1 + {\rm Int} \times {\rm Int} \to {\rm Int}$ となります。f としては以下の様な関数 plus が考えられます。もちろんこれ以外にも様々な f の実装が考えられます。

plus :: F Int -> Int
plus Nil = 0
plus (Cons a b) = a + b

特にF-代数の中で、任意の他のF-代数への準同型が一意に存在するものを F-始代数 (initial F-algebra) といいます。⁵ つまり、先の図において、任意の型 $B$ に対し $f$ が一意に存在する場合、$A$はF-始代数になります。

さて、実は $(\mu F, {\sf inF})$ は F-始代数であることが知られています。⁶つまり、任意のF-代数 $(X, \varphi : F(X) \to X)$ に対して関数 $f : \mu F \to X$ が一意に存在します。この時、$f$ のことを catamorphism ⁹ と呼びます。また、$f$ を ${\sf cata} \varphi$ や $ (\!| \varphi |\!) $ と表すこともあります。

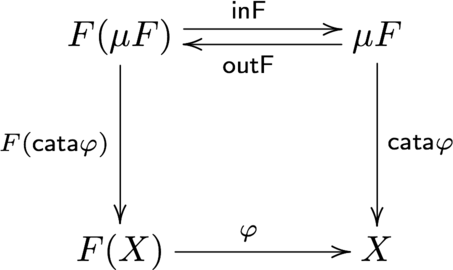
図式が示すように、catamorphism は以下のように表現できます。

これをHaskellのコードにすると以下のようになります。引数として関数 $ \varphi : F(A) \to A $ を受け取り「$\mu F$ を受け取り A を返す関数」を返す、高階関数になっています。

cata :: Functor f => (f a -> a) -> FixF f -> a
cata phi = phi . fmap (cata phi) . outF

catamorphism は、いわゆる関数型プログラミングにおける fold の一般化です。関手$F$ がリストを構成するならリストの畳込みを意味し、木を構成するなら木の畳み込みを意味します。 つまり、catamorphismは関手$F$によって構成されたデータ構造を次々と畳み込んで、一つの値に収束させることを意味しています。

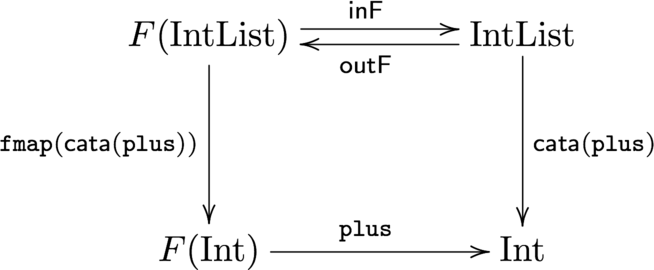
catamorphism を使ってリストの畳込みをしてみます。 既にこれまで定義した関数や型を用いています。

-- リストの総和を求める関数
sumIL :: IntList -> Int
sumIL = cata plus where
  plus :: F Int -> Int
  plus Nil = 0
  plus (Cons a b) = a + b
  -- ここで a は 今見ているリストの先頭、b はこれまでの畳込みの結果を表している

{-
main = print $ sumIL $ cons 100 $ cons 20 $ cons 3 $ nil
出力: 123
-}

この時の状況は以下のようになっています。

3.2. 余代数とanamorphism

余代数(coalgebra)とは、代数の双対です。つまり、先ほどの可換図式の矢印を反対したものが、そのまま余代数になります。

一応定義を書いておきます。関手 $F$ について、型 $A$ と、関数 $f : F(A) \to A$ のペア $(A, f)$ を $F$-余代数 (F-coalgebra) といいます。 また、F-余代数 $(A, a : A \to F(A)), (B, b : B \to F(B))$ に対し、$f : A \to B$ で $F(f) \circ a = b \circ f$ を満たすものをF-余代数の準同型 (homomorphism of F-coalgebra) といいます。すなわち、以下の図式を可換にします。

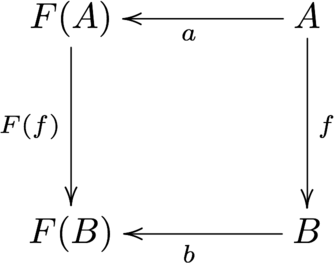
特にF-余代数の中で、任意の他のF-余代数からの準同型が一意に存在するものを F-終余代数 (terminal F-coalgebra) といいます。⁷ つまり、先の図において、任意の型 $A$ に対し $f$ が一意に存在する場合、$B$はF-終余代数になります。

先程と同様に、$(\mu F, {\sf outF})$ は F-終余代数であることが知られています。⁸つまり、任意のF-余代数 $(Y, \psi : Y \to F(Y))$ に対して関数 $f : Y \to \mu F$ が一意に存在します。この時、$f$ のことを anamorphism ¹⁰ と呼びます。また、$f$ を ${\sf ana} \psi$ や $ [\!( \psi )\!] $ と表すこともあります。

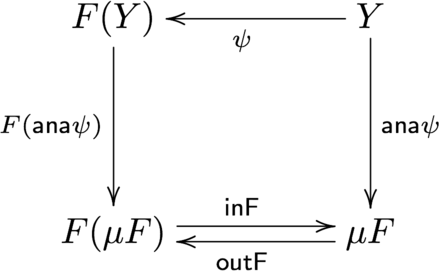
図式が示すように、anamorphism は以下のように表現できます。

Haskell のコードで実装すると以下のようになります。

ana :: Functor f => (a -> f a) -> a -> FixF f
ana psi = InF . fmap (ana psi) . psi

catamorphism が 「データ構造を畳み込んで一つの値にしていくもの」ものとは逆に、anamorphism は「一つの値からデータ構造を構築していくもの」といえます。つまり、ある初期値 $a$ (seed と呼ばれることがあります) が ${\sf ana} \psi$ に与えられると、$\psi$ が次々に適用され、無限(もしくは有限)の大きさのリストや木などのデータ構造が得られます。 Haskell ではリストに対する anamorphism として unfoldr というものが Data.List に定義されています。

さて、anamorphism の例を見てみましょう。ここでは0からn-1まで1ずつ増加していくリストを構築する関数 iota を考えてみます。

iota :: Int -> IntList
iota n = (ana psi) 0 where
  psi :: Int -> F Int
  psi i = if i == n then Nil
                    else Cons i (i + 1)
  -- Cons の第一引数はリストの要素の値、第二引数は次のphiの引数に渡す値となる

--- iota 3 == cons 0 $ cons 1 $ cons 2 $ nil

4. hylomorphism

hylomorphism とは、まず anamorphism によってデータ構造を構築し、catamorphism により生成したデータ構造を畳み込んで一つの値にする一連の処理を行う関数です。これは2つの合成関数として表現できます。

これを図式に表すと以下のようになります。

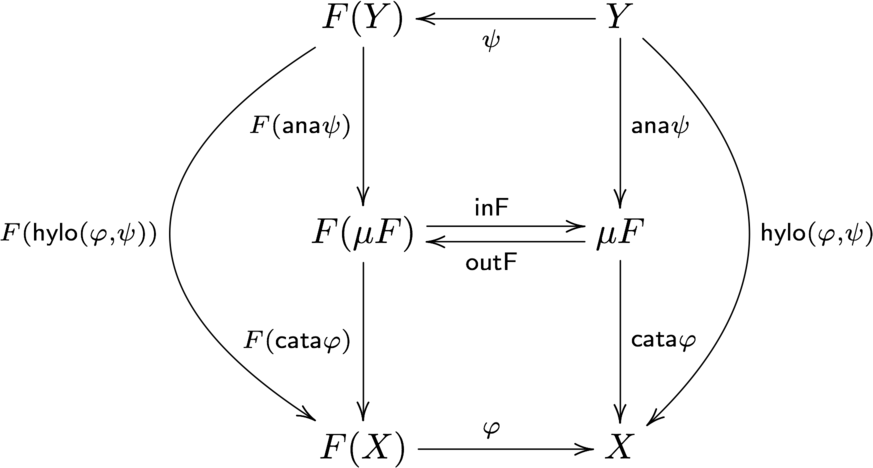
図式を見てわかるように、hyloは以下のようにも書けます。

さて、hyloをHaskellに実装すると以下のようになります。

hylo :: Functor f => (f x -> x) -> (y -> f y) -> (y -> x)
hylo phi psi = cata phi . ana psi

hylomorphism によって、再帰関数の処理が表現できます。再帰関数の呼び出しは、call treeという木構造で表現できます。そのため、${\sf ana} \varphi$で引数の値に基づきそのcall treeを再現し、さらにその tree を evaluation する処理を ${\sf cata} \psi$ で行えば、再帰関数と同等の処理が可能になります。

では再帰関数の例としてフィボナッチ数列のn番目を求める関数 $fib(n)$ をhyloで実現しましょう。この時 hylo のベースになる関手 $F_{fib}(X)$ は、$F_{fib}(X) = 1 + 1 + Int \times X \times X$ となります。

この時 $1 + 1$ は再帰関数の「底」、つまり $fib(0) = 0$ と $fib(1) = 1$ を意味しています。また、$X \times X$ は $fib(n) = fib(n-1) + fib(n-2)$ の2つの fib 関数の呼び出しを表現しています。したがって、この関手の不動点 $\mu F_{fib}$ は、fib の call tree (二分木) を表す再帰的データ構造になります。

{- fibのcall-treeを構築する関手 -}
data FibT a = FZero | FOne | FNode a a
{- FibTは関手のインスタンスである -}
instance Functor FibT where
  fmap _ FZero = FZero
  fmap _ FOne  = FOne 
  fmap f (FNode a b) = FNode (f a) (f b)

fibAsHylo :: Int -> Int
fibAsHylo = hylo phi psi where
  {- fibのcall-treeを構成する -}
  psi :: Int -> FibT Int
  psi 0 = FZero -- f(0) [葉]
  psi 1 = FOne  -- f(1) [葉]
  psi n = FNode (n - 1) (n - 2) -- f(n-1), f(n-2) を子にする枝

  {- 作られた call-tree を評価する -}
  phi :: FibT Int -> Int
  phi FZero = 0 -- f(0) = 0
  phi FOne = 1 -- f(1) = 1
  phi (FNode a b) = a + b -- f(n - 1) + f(n - 2)

{-
main = print $ fibAsHylo 10
結果: 55
-}

これで再帰関数をhyloで表せることが分かりました。しかしこの場合、引数の値が大きくなるにつれ、ana によって作られる中間データ構造の大きさが指数的に増えていきます。これは一般に再帰関数のcall-treeが指数的に大きくなるのと同じ現象です。

普通、再帰関数が指数的に増えないようにするためには、メモ化などの技法が考えられます。そして、hyloについても同様にメモ化を考えることができ、それがずばりdynamorphismなのですが、dynamorphism を導入する前にまず histomorphism について解説します。

5. histomorphism

histmorphism は catamorphism の拡張であり、catamorphismは直前の結果しか参照できなかったものを、過去の任意の時点での結果を参照できるようにしたものです。 これを実現するためには、過去の値を保持できるようなデータ構造を作らなければなりません。以下ではまず与えられた関手Fに対してそのようなデータ構造を構成する方法を示し、その上で histmorphism を定義します。

5.1. $F^{\times}_A$ と $\tilde{F}$

関手 $F$ と 型 $A$ について、 $F^{\times}_A$ を以下の様に定義します。

$F^{\times}_A(X)$ は、F(X) に 型 A の情報(タグ)を付加したものとみなすことが出来ます。

さらに、$F^{\times}_A(X)$を用いて、${\tilde F}(X)$ を以下のように定義します。

$ ana(-)_{F^{\times}_A} $ は $ { F^{\times}_A } $ -余代数における anamorphism です。 $\epsilon, \theta$ は後に述べます。

さて、${\tilde F}(A)$ はどういう意味なのでしょうか。 原論文(参考文献[1])にはこうあります。

${\tilde F}(A)$ a datatype of $F$-branching trees, where every node is annotated by values of type A.

つまり、例えば 関手$F(X)$ が木を構成するならば、${\tilde F}(A)$は木の全てのノードに型 A の値が付加されたデータ構造になります。 次の章に登場する histomorphism では、このAの部分に途中の計算結果を格納することによって、その結果を後から再利用することを可能にしています。 以下、${\tilde F}(A)$が表すデータ構造を${\tilde F}$-treeと表現します。

特に $A = 1$ である場合、つまり付加する情報がない場合 ${\tilde F}(1) = \mu F$ となり $F(X)$ によって構成されるデータ構造と同型になります。

ここで${\tilde F}$についての関数 $\epsilon, \theta$ が登場します。$\epsilon$は ${\tilde F}(A)$ を受け取り、付加された型$A$の値 を取り出す関数です。後のコードでは extract という名前で定義します。 また、$\theta$ は、${\tilde F}(A)$ を受け取り、$F({\tilde F}(A))$を返します。これは元の(F(X)によって構成された)木構造を取り出す関数です。後のコードでは sub という名前です。

実際のHaskellでの実装は以下のようになります。なお、$F^{\times}_A(X)$は Fx、${\tilde F}(X)$のことを Cofree という名前にしています。¹²

-- Fx = A × F(X)
data Fx f a x = FCons a (f x)
instance Functor f => Functor (Fx f a) where
  fmap f (FCons x xs) = FCons x (fmap f xs)

-- Cofree の宣言
newtype Cofree f a = Cf { unCf :: FixF (Fx f a) }

-- Cofree が関手に成るための宣言
instance Functor f => Functor (Cofree f) where
  fmap f = Cf . ana (phi . outF) . unCf where
    phi (FCons a b) = FCons (f a) b

-- ノードの付加情報を取り出す
extract :: Functor f => Cofree f a -> a
extract cf = case (outF $ unCf cf) of
  FCons a _ -> a

-- ノードを取り出す
sub :: Functor f => Cofree f a -> f (Cofree f a)
sub cf = case (outF $ unCf cf) of
  FCons _ b -> fmap Cf b

5.2. histomorphism

前述したように、関手$F$に対する${\tilde F}$とは、Fによる再帰的データ構造のそれぞれのノードに値を付加できるようにしたものです。そこへ結果を格納することによって、後の任意の時点でその計算結果を参照することが可能になります。以下、histmorphismの定義からはじめます。

$F{\tilde F}$-代数 $(F{\tilde F}A, \varphi : F{\tilde F}A \to A)$ に対して、histomorphism は以下の図式を可換にするような一意な関数 ${\sf histo}(\varphi)$ のことを言います。

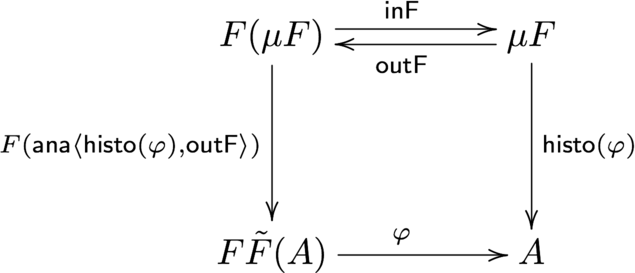
histmorphism は、${\tilde F}$ -tree に対する catamorphism であると喩えることができます。

先程のhistoの定義をHaskellで実装すると以下のようになります。

histo :: Functor f => (f (Cofree f a) -> a) -> FixF f -> a
histo phi = phi . (fmap (Cf . (ana proj))) . outF where
  proj a = FCons (histo phi a) (outF a)

また、histoの表現は他にもあります。¹³

(12) がどう導かれるかは以下の図式を辿ってみれば分かると思います。

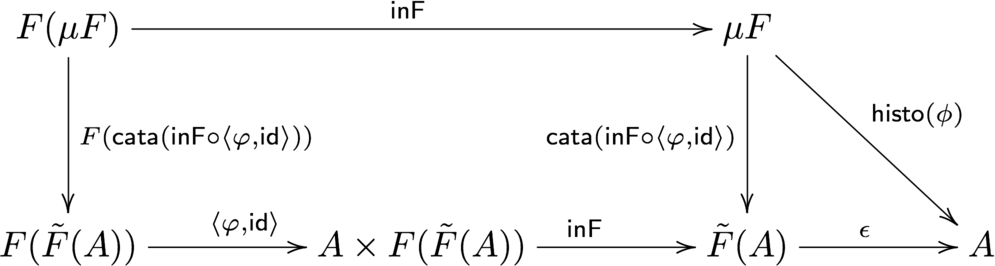
(12) をHaskellで実装すると以下のようになります。

histo' :: Functor f => (f (Cofree f a) -> a) -> FixF f -> a
histo' phi = extract . cata ap where
  ap a = Cf $ InF $ FCons (phi a) (fmap unCf a)

さて、histomorphism を用いた例を見てみましょう。ここでは再度フィボナッチ数列のn番目を返す関数 $fib(n)$ を考えます。histomorphism は、引数としてデータ構造を取るため、別途引数として渡すためのデータ構造を作っておく必要があります。

-- 関手 TNat(X) = 1 + X、整数を構成する
data TNat a = Zero | Succ a
instance Functor TNat where
  fmap f (Succ a) = Succ $ f a
  fmap _ Zero     = Zero

-- 正の整数を表現するデータ型 Nat = μTNat
type Nat = FixF TNat

-- 整数型からNatへ変換する関数
nat :: Integer -> Nat
nat 0 = InF Zero
nat n = InF $ Succ $ nat $ n - 1

-- フィボナッチ数列を求める
fibAsHisto :: Nat -> Integer
fibAsHisto = histo' phi where
  phi Zero = 0 -- (a)
  phi (Succ x) = f1 + f2 where -- (b)
    f1 = extract x
    f2 = case sub x of
      Zero   -> 1 -- (c1)
      Succ y -> extract y -- (c2)

main = print $ fibAsHisto $ nat 100

fibAsHisto の入力は、関手 TNat によって構成されるデータ構造 $\mu TNat$ になります。ここで $TNat(X) = 1 + X$ であり、型レベルで自然数を構成しています。

phi について、 (a) は 引数に 0 が来た時に 0 を返すことを表しています。引数に 1 以上が来た時は、fib(i-1) + fib(i-2) を計算します (b)。

f1 は 現在のノードの付加情報を取り出しています。これは直前の結果が入っており、これがf(i-1)を表現しています。 また、f2では${\tilde F}$-tree の子ノード (subtree) を遡って2つ前の結果 f(i-2) を取り出しています (c2)。ただし subtree が遡れない場合は、1を返しています(c1)。これが fib(1) を表しています。

fibAsHylo に比べ fibAsHisto は実行速度が著しく上がっています。これは過去の結果を再利用することで、同じ計算を繰り返さずにすむようになったからです。

6. dynamorphism

dynamorphism は、histomorphism の前に anamorphism をつなげたものです。つまり、anamorphism でデータ構造を構築し、histomorphism でそれを畳み込む一連の処理を行います。これは hylomorphism の考え方と同じです。よって、dynamorphism は プリミティブな型(整数や文字列など) を受け取りプリミティブな型を返す関数となり、関数を呼び出す側からは中間のデータ構造を意識する必要がなくなります。

dynamorphism の定義は以下のようになっています。¹⁴

また、hylo を用いて以下のようにも表せます。

(14) は (7), (12), (13) から自明に導かれます。

(14) を Haskell で実装すると以下のようになります。

dyna :: Functor f => (f (Cofree f x) -> x) -> (y -> f y) -> (y -> x)
dyna phi psi = extract . hylo ap psi where
  ap a = Cf $ InF $ FCons (phi a) (fmap unCf a)

dynamorphism の例を上げます。fibについては先ほどの fibAsHisto に若干の変更を加えるだけなので簡単です。ここでは動的計画法の典型的な例である「0-1ナップサック問題」を実装してみます。

0-1 ナップサック問題とは、

容量 c のナップサックが一つと、n個の品物（それぞれ 価値 v[i], 容積 w[i]）が与えられたとき、ナップサックの容量 c を超えない範囲で価値を最大にするように品物を詰めた時、価値の総和はいくつになるか。

という問題です。

この問題は動的計画法で厳密解が求まります。$dp[i][j]$ を 「i番目以降の品物から容量jでの最大値となるように選んだ時の価値の和」とすると、

としたときの $dp[0][c]$ が解となります。

さて、これを dynamorphism で実装してみます。以下がコードです。

-- psi によって作られる中間データ構造、(Int, Int) のフィールドを持ち、dp[i][j] のインデックス i,j を表現している。
data KSTree a = KSTree (Int, Int) (Maybe a)
instance Functor KSTree where
  fmap f (KSTree a Nothing)  = KSTree a Nothing
  fmap f (KSTree a (Just b)) = KSTree a (Just (f b))

{- 0-1ナップザック問題を解く。c は全重量の制約、vは品物の価値のリスト、wは重量のリスト -}
knapsack :: Int -> [Int] -> [Int] -> Int
knapsack c v w = dyna phi psi $ (n,c) where
  n = length w -- 品物の数

  psi (0,0) = KSTree (n,0) Nothing
  psi (0,j) = KSTree (n,j) (Just (n, j-1))
  psi (i,j) = KSTree (n-i,j) (Just (i-1, j))

  phi (KSTree _ Nothing) = 0
  phi (KSTree (i,j) (Just cs))
    | i == n      = 0
    | w !! i <= j = max x1 x2
    | otherwise   = x1
    where
      x1 = back 1 cs
      x2 = (v !! i) + (back (1 + (n + 1) * (w !! i)) cs)

  {- 過去の結果を遡って参照するための関数 -}
  back 1 cs = extract cs
  back i cs = case sub cs of
    (KSTree _ (Just b)) -> back (i - 1) b

main = show $ knapsack 5 [4,2,5,8] [2,2,1,3] -- 13

さて、順番に見ていきましょう。

  psi (0,0) = KSTree (n,0) Nothing
  psi (0,j) = KSTree (n,j) (Just (n, j-1))
  psi (i,j) = KSTree (n-i,j) (Just (i-1, j))

psi 関数をanaに渡すことで中間データ構造を生成します。サンプル入力の場合、以下のようなリスト(型はFixF KSTree)を出力します。 これは $dp[i][j]$ の全てのインデックスを列挙したものになっています。

(0,5),(1,5),(2,5),(3,5),(4,5),
(0,4),(1,4),(2,4),(3,4),(4,4),
(0,3),(1,3),(2,3),(3,3),(4,3),
(0,2),(1,2),(2,2),(3,2),(4,2),
(0,1),(1,1),(2,1),(3,1),(4,1),
(0,0),(1,0),(2,0),(3,0),(4,0)

これを一分木とみなすと、ルートノードは(0,5)で終端の葉は(4,0)であり、各々のノードに対し子ノードはリストの次の要素になります。 この後のhisto(phi)によりこのデータ構造が畳み込まれます。

次に畳み込む部分を見てみます。

  phi (KSTree _ Nothing) = 0 -- (a)
  phi (KSTree (i,j) (Just cs))
    | i == n      = 0 -- (b)
    | w !! i <= j = max x1 x2 -- (c)
    | otherwise   = x1 -- (d)
    where
      x1 = back 1 cs
      x2 = (v !! i) + (back (1 + (n + 1) * (w !! i)) cs)

4つの場合分けを行っています。

まず(a)についてですが、これは終端の葉の時、つまり (4,0) が渡された時のものです。もちろんこれは0を返すことになります。 (b)についても同様に、(15) の定義通り i = n の時は 0 を返します。

問題は(c),(d)の部分です。 (15) と比較することによって、x1 が $dp[i+1][j]$、x2 が $dp[i+1][j-w[i]]+v[i]$ であることが推測できます。x1, x2 では back という関数を使っています。

  {- 過去の結果を遡って参照するための関数 -}
  back 1 cs = extract cs
  back i cs = case sub cs of
    (KSTree _ (Just b)) -> back (i-1) b

この back は 引数 i を与えると、現在時から i 時点前 (すなわち${\tilde F}$-treeにおけるi代目の子孫ノード) の結果を取得して返してきます。 つまり、リスト 18 においては、現在 cs が (i,j) のノードであるとすると、back 1 cs は (i-1,j) の時点の結果を返し¹⁵、back (1 + (n + 1) * (w !! i)) cs は (i-1,j-w[i]) ¹⁶ 時点の結果を返すことになります。よって先ほどの推測は正しく、(15) を実装できたことが確認できました。

一応畳み込む際の途中計算の結果を示しておきます。(実際には呼ばれない部分にも値が入っています)余裕があれば手で追ってみてください。

13:(0,5) 13:(1,5) 13:(2,5) 8:(3,5) 0:(4,5)
13:(0,4) 13:(1,4) 13:(2,4) 8:(3,4) 0:(4,4)
 9:(0,3)  8:(1,3)  8:(2,3) 8:(3,3) 0:(4,3)
 5:(0,2)  5:(1,2)  5:(2,2) 0:(3,2) 0:(4,2)
 5:(0,1)  5:(1,1)  5:(2,1) 0:(3,1) 0:(4,1)
 0:(0,0)  0:(1,0)  0:(2,0) 0:(3,0) 0:(4,0)

7. まとめ

• 再帰的データ構造は関手の不動点で表せます。
• F-代数 とは、型と関数のペア $(A, f : F(A) \to A)$ のことを言います。その双対であるF-余代数 は $(B, g: B \to F(B))$ です。(余)代数間で構造を保つ写像を準同型 といいます。
• F-代数において $(\mu F, {\sf inF})$ からの準同型 のことを catamorphismといいます。これはデータ構造の畳込みを行います。
• F-余代数において $(\mu F, outF)$ への準同型 のことを anamorphismといいます。これはデータ構造の構築を行います。
• hylomorphism は anamorphism が出力したデータ構造を catamorphism に入力して得られる結果を返します。
• ${\tilde F}(A)$ とは、$\mu F$ のそれぞれのノードに 情報 $A$ を付加したものです。
• histmorphism は、関手 $F$ に対して ${\tilde F}$ を考え、その上の catamorphism を行います。
• dynamorphism は、anamorphism が出力したデータ構造を histmorphism に入力して得られる結果を返します。

8. あとがき

今回は catamorphism, anamorphism, histmorphism, dynamorphism について説明しました。しかし -morphism は他にもあります。 histmorphism の双対である futumorphism、その2つを繋げた chronomorphism、hylomorphism での ana, cata の関数合成を逆にした metamorphism また catamorphism を拡張した paramorphism, zygomorphism, prepromorphism、それらの双対である apomorphism, cozygomorphism, postproporphism、 他にも synchromorphism や exomorphism や mutumorphism などもあります。これらの morphism (まとめて recursion schemes と呼ばれます)は Haskell では recursion-schemes などに実装されています。

以上 dynamorphism とそれに至る経緯について長々と説明してきました。しかし説明が不十分であったり分かりにくい所も多いと思います。その際は、原論文 (参考文献[1])を当たったり、実際に自分の手で実装したりしてみてください。

また、今回の話は圏論について余り触れませんでした。圏論は抽象的で難しくて役に立つかわからないと思うかもしれませんが、主に関数型プログラミングなどの計算機科学の論文を当たると、圏論を用いて明快な結果を出しているものも多いです。最近圏論に関する本やネットの記事も増えてきているので、一度触れてみてはどうでしょうか。

9. 参考文献

1. Jevgeni Kabanov and Varmo Vene. 2006. Recursion schemes for dynamic programming. In Proceedings of the 8th international conference on Mathematics of Program Construction (MPC'06), Tarmo Uustalu (Ed.). Springer-Verlag, Berlin, Heidelberg, 235-252.

   dynamorpism の初出論文です。この記事とだいたい同じ流れ(cata, ana, histo から dynamorpism に至る)で構成されています。dynamorphismを利用した例として編集距離やLCSの例が挙げられています。

2. Ralf Hinze and Nicolas Wu. 2013. Histo- and dynamorphisms revisited. In Proceedings of the 9th ACM SIGPLAN workshop on Generic programming (WGP '13). ACM, New York, NY, USA, 1-12.

   dynamorphism に触れている2つめの論文です。この論文では Comonad や λ-bicategory などを用いてより高度な議論をしています。サンプルコードとしてカタラン数や制限巡回セールスマン問題などを挙げています。

3. Madoko Reference : この文章は madoko を用いて生成されました。madoko は Markdown を学術論文向けに拡張し、PDF(LaTeX経由)やHTMLを出力します。開発者はMSRの人のようです。
4. 代数的データ型について #w8lt // Speaker Deck : 代数的データ型がなぜ代数と呼ばれるかという疑問からF-代数に至るまでのスライドです。W8LTは東京工業大学という大学のの西8号館と呼ばれる建物で行われたライトニングトークを指すようです。
5. Computes Fibonacci number with a histomorphism – correction: Actually it's a dynamorphism as it uses an anamorphism to generate intermediary step : 関数 fibAsHisto を作成する際に参考にしました。
6. 動的計画法（ナップサック問題） - アルゴリズム講習会 : DP の式などを参考にしました。
7. XY-pic : 可換図式を作成する際に参考にしました。
8. nLab : 圏論に関する百科事典です。
9. 圏論勉強会 第10回 @ ワークスアプリケーションズ : F-代数について分かりやすく説明しています。圏論勉強会の他のスライドもおすすめです。実は僕も2年前にこの勉強会に参加していました。
10. 万物の創造 : 東京工業大学 ロボット技術研究会
11. The Comonad.Reader » Recursion Schemes: A Field Guide (Redux)